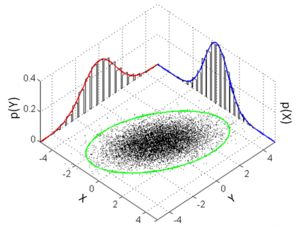
Goal

The goal for this post is to introduce and to write two parametric classifiers by modeling each class’s conditional distribution $p(x|C_i)$ as multivariate Gaussians with (a) full covariance matrix $\Sigma_i$ and (b) diagonal covariance matrix $\Sigma_i$. numpy will be the only package allowed to use since I decide to code from the ground.

Multivariate Gaussian Classifer

As before we use Bayes’ theorem for classification, to relate the probability density function of the data given the class to the posterior probability of the class given the data. Let’s consider d-dimensional data x from class C modelled using a multivariate Gaussian with mean $\mu_i$ and variance $\Sigma_i$. Using Bayes’ theorem we can write:

$$\begin{aligned} p(\mathbf{x} | C)=p(\mathbf{x} | \mu, \mathbf{\Sigma})=\frac{1}{(2 \pi)^{d / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{T} \mathbf{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right) \end{aligned}$$

The log likelihood is: $$L L(\mathbf{x} | \mu, \Sigma)=\ln p(\mathbf{x} | \mu, \Sigma)=-\frac{d}{2} \ln (2 \pi)-\frac{1}{2} \ln |\Sigma|-\frac{1}{2}(\mathbf{x}-\mu)^{T} \Sigma^{-1}(\mathbf{x}-\mu)$$

And we can write the log posterior probability:

$$\ln P(C | \mathbf{x})=-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{T} \mathbf{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})-\frac{1}{2} \ln |\mathbf{\Sigma}|+\ln P(C )+\mathrm{const.}$$

Idea

By using the training data, I will need to compute the maximum likelihood estimate of the class prior probabilities $p(C_i)$ and the class conditional probabilities $p(x|C_i)$ based on the maximum likelihood estimates of the mean $\mu_i$ and the (full/diagonal) covariance $\Sigma_i$ for each class $C_i$. The classification will be done based on the following discriminant function: $$g_i(x) = log p(C_i) + log p(x|C_i) $$

Code

The code can be divided into 3 parts:

fit(self,X,y,diag): the inputs (X; y) are respectively the feature matrix and class labels, and diag is boolean (TRUE or FALSE) which indicates whether the estimated class covariance matrices should be a full matrix (diag=FALSE) or a diagonal matrix (diag=TRUE).

predict(X): the input X is the feature matrix corresponding to the test set and the output should be the predicted labels for each point in the test set.

_init_ (self,k,d): It initialize the parameters for each class to be uniform prior, zero mean, and identity covariance.

Here is the code

Performance

For checking the performance of this classifier, I use the digits dataset from sklearn. Also, I use logistic regression for comparison

Here are the ROC curves for three classifiers.

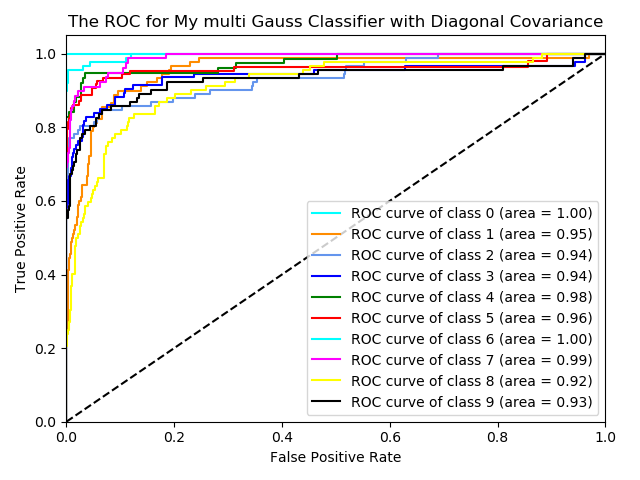
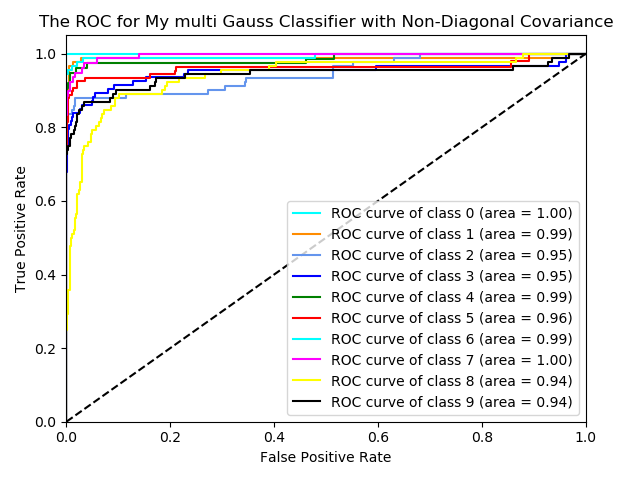
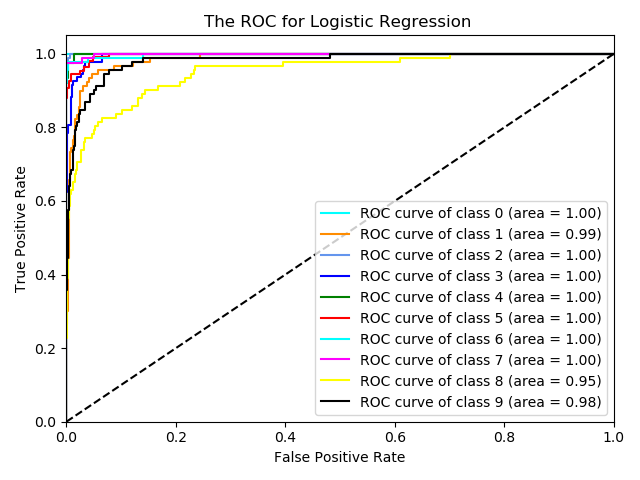
From the graphs, it looks like the classifier with the Non-diagonal covariance has better performance than the diagonal one. It means some features are dependent among all 64 features. Also, the logistic regression has a relatively better performance than the Multivariate Gaussian Classifer.